동적 계획법(Dynamic Programming)

13 Aug 2017

동적 계획법이란?

동적 계획법(dynamic programming)은 최적화 문제를 풀기 위해 고안된 기법으로 복잡한 문제를 보다 간단한 여러 개의 부분 문제로 나누어 해결한다. 중요한 점은 한 번 계산한 부분 문제의 답을 저장해 두어 나중에 같은 부분 문제의 답을 이용할 때, 복잡한 연산 없이 바로 이용할 수 있도록 하는 것이 핵심이다. 주로 중복되는 부분 문제(overlapping sub-problems)와 최적 부분 구조(optimal substructure)를 가지고 있는 문제들을 풀때 사용된다. 보다 자세한 내용은 뒤에 후술한다.

동적 계획법을 이용한 알고리즘을 설계할 때 가장 중요한 것은 현재 문제의 상태(state)와 현재 문제와 부분 문제간의 관계(relationship) 또는 전이(transitions)를 파악하는 것이다. 문제들간의 관계 또는 전이를 정확하게 파악하면 알고리즘의 정당성을 얻을 수 있고, 동적 계획법 알고리즘의 시간복잡도는 상태의 수와 한 상태의 답을 결정짓기 위한 시간에 비례하므로 이를 잘 고려하여 문제간의 상태와 관계를 잘 파악하는 것이 중요하기 때문이다.

중복되는 부분 문제(Overlapping subproblems)

주어진 문제를 여러 개의 부분 문제로 나누어 풀 때, 같은 부분 문제의 답을 여러 번 계산하는 경우가 있을 수 있다. 이런 부분 문제들을 중복되는 부분 문제 (overlapping subproblems)라고 한다. 동적 계획법에서는 이런 중복되는 부분 문제들을 단 한번만 계산하여 알고리즘의 속도를 최적화한다. 예를 들어 이항 계수(binomial coefficient)를 구하는 문제를 보자. 이항 계수 \(\binom n r\)은 \(n\)개의 서로 다른 원소 중에서 \(r\)개의 원소를 순서없이 고르는 방법의 수로, 다음과 같은 점화식(파스칼의 법칙)이 성립한다.

\(\binom n r = \binom {n-1} {r-1} + \binom {n-1} r\)

위 점화식을 토대로 \(\binom 4 2\)를 재귀적으로 구한다고 하면 아래 왼쪽 그림과 같이 \(\binom 2 1\)을 구하는 과정이 중복된다는 사실을 인지할 수 있다. 사람이 직접 계산할 때에는 문제가 중복됨을 바로 인지하여 한 번만 계산할 수도 있겠지만 컴퓨터는 그렇지 못한다. 아래 오른쪽 그림과 같이 중복되는 부분 문제를 단 한번만 계산하도록 하는 것이 동적 계획법의 핵심이다.

overlapping-subproblems

최적 부분 구조(Optimal substructure)

동적 계획법을 최적화 문제 풀이에 적용하려면, 주어진 문제에 중복되는 부분 문제 말고도 최적 부분 구조 (optimal substructure)라는 특성이 필요하다. 어떤 문제가 최적 부분 구조를 가진다는 것은 주어진 문제의 최적해를 그 문제의 부분 문제들의 최적해를 통해 얻을 수 있다는 것을 말한다. 예를 들어 아래 그림과 같이 서울에서 부산으로 가는 최단 경로 문제를 보자.

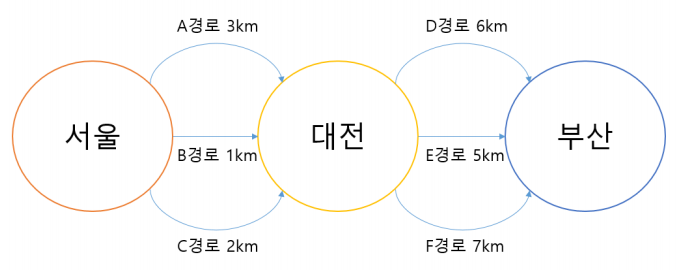
서울에서 부산으로 갈 때 반드시 대전을 지난다고 가정하면, 이 경로를 (서울 -> 대전)과 (대전 -> 부산)으로 나눌 수 있다. 그러면 두 구간의 최단 경로(각각 1km, 5km)를 찾아 둘을 이으면 항상 서울에서 부산으로 가는 최단 경로(6km)를 얻을 수 있게 된다. 이런 경우 전체 문제의 최적해(최단 거리)가 부분 문제들의 최적해를 통해 얻을 수 있으므로 최적 부분 구조를 가진다고 할 수 있다. 이러한 특성이 모든 최적화 문제에 성립하는 것은 아니다. 위의 문제에서 경로상에 통행료와 같은 다른 제약이 존재하고, 총 통행료 합이 얼마 이하여야만 한다는 특정 상황이 추가된다면 위에서 당연한 듯 보였던 최적 부분 구조는 성립하지 않게 된다. 따라서 동적 계획법을 최적화 문제 풀이에 적용하려면, 주어진 문제에 최적 부분 구조가 성립하는지를 잘 따져봐야 한다.

경우의 수와 확률(Counting and Probability)

동적 계획법은 초기에 최적화 문제를 풀기 위해 고안되었지만 앞서 설명한 이항 계수를 구하는 문제와 같이 경우의 수를 세거나 확률을 계산하는 문제에서도 흔하게 사용된다. 경우의 수를 세는 문제들은 대게 재귀적인 특성을 가지고 있어 중복되는 부분 문제가 많고, 최적화 문제의 최적 부분 구조와 유사하게 어떤 문제의 경우의 수가 그 문제의 부분 문제들의 경우의 수들의 조합일 때가 많기 때문이다.

동적 계획법의 구현(Top-Down vs Bottom-Up)

동적 계획법 알고리즘을 설계하였다면, 즉 문제의 상태와 문제들간의 관계 파악이 끝났다면 이를 코드로 구현해야 한다. 보통 두 가지 방식을 사용한다. 하나는 재귀 함수를 이용한 Top-Down 방식이고, 다른 하나는 반복문을 통해 DP 테이블을 채워나가는 Bottom-Up 방식이다. 두 방식 모두 각각의 장단점이 있으므로 문제의 특성을 고려하여 잘 선택하면 된다.

재귀 함수를 이용한 구현(Top-Down DP)

재귀 함수를 이용한 구현은 대체로 직관적으로 와닿는다. 동적 계획법으로 해결할 수 있는 아주 간단한 문제중 하나인 피보나치 수열을 구하는 문제를 보자. 피보나치 수는 다음과 같이 정의되는 수열이다.

\[F_0=0, F_1=1\] \[F_n=F_{n-1}+F_{n-2}\]

n번째 피보나치 수는 재귀적으로 해결할 수 있음을 알 수 있다. 따라서 다음과 같이 구현할 수 있다.

int dp[MAX_N]; // initially set all -1

int fibo(int n) {
  if (n <= 1) return n;
  int& ret = dp[n]; // memoization
  if (ret != -1) return ret;
  return fibo(n - 1) + fibo(n - 2);
}

재귀 함수를 이용한 구현에서 눈여결 볼 부분은 메모이제이션(memoization) 부분이다. 메모이제이션 부분이 없다면 같은 부분 문제를 너무 많이 중복해서 계산하게 된다. 이러한 중복 계산을 방지하기 위해 한 번 계산해둔 부분 문제의 답은 기억해두고 다시 한 번 그 부분 문제의 답을 계산해야 하는 순간이 오면 기억해 둔 답을 바로 반환하면 된다.

반복문을 이용한 구현(Bottom-Up DP)

반복문을 이용한 구현은 부분 문제들간의 의존성을 파악하여 먼저 해결되어야 할 부분 문제부터 풀어나간다. 위에서 보았던 피보나치 수를 구하는 문제는 다음과 같이 구현할 수 있다.

int fibo2(int n) {
  int dp[n + 1];
  dp[0] = 0;
  dp[1] = 1;
  for (int i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
}

이와 같이 각 부분 문제의 답에 해당하는 dp 배열을 반복문으로 채워나가는 방식이 표를 채워나가는 것처럼 보여서 Tabulation이라고도 한다.

두 방식의 비교

	Top-Down DP(Memoization)	Bottom-Up DP(Tabulation)
장점	1. 대체로 코드를 직관적으로 이해할 수 있다.	1. 대체로 Top-Down 방식보다 빠르다.
	2. 필요한 부분 문제만을 계산한다. (이로 인해 종종 Bottom-Up 방식보다 빠를때도 있다.)	2. 슬라이딩 윈도우 기법을 사용하여 메모리 사용량을 절약하는 기법을 사용할 수 있을 때도 있다.
단점	1. 함수 호출 및 반환 방식으로 인한 오버헤드 때문에 Bottom-Up 방식에 비해 느리다.	1. 부분 문제들간의 의존성 파악을 정확하고, 이에 맞게 정확하게 DP 테이블을 채워나가야 한다.
	2. 가끔 메모리 제한이 엄격한 문제를 해결하지 못할 가능성이 있다.

연습 문제

BOJ 2156 포도주 시식 (문제 보기)

BOJ 2507 공주 구하기 (문제 보기)

BOJ 10272 현상금 사냥꾼 김정은 (문제 보기)

BOJ 2618 경찰차 (문제 보기)

BOJ 9023 연습시즌 (문제 보기)

BOJ 2293 동전 1 (문제 보기)

BOJ 2294 동전 2 (문제 보기)

BOJ 11049 행렬 곱셈 순서 (문제 보기)

BOJ 11066 파일 합치기 (문제 보기)

BOJ 1912 연속합 (문제 보기)

CF 835C Star sky (문제 보기)

BOJ 1005 ACM Craft (문제 보기)

BOJ 2533 사회망 서비스(SNS) (문제 보기)

BOJ 2213 트리의 독립집합 (문제 보기)

BOJ 2266 금고 테스트 (문제 보기)

BOJ 13308 주유소 (문제 보기)

최적해 구성하기

BOJ 2662 기업 투자 (문제 보기)

BOJ 2618 경찰차 (문제 보기)

k번째 사전순 답(k-th lexicographical string)

BOJ 1023 괄호 문자열 (문제 보기)

AOJ KLIS K-th Longest Increasing Sequence (문제 보기)

AOJ DRAGON 드래곤 커브 (문제 보기)

비트마스크(Bitmask)

BOJ 2098 외판원 순회 (문제 보기)

BOJ 1014 컨닝 (문제 보기)

BOJ 1029 그림 교환 (문제보기)

부분 상태 + Exponential Search

BOJ 11438 LCA2 (문제 보기)

BOJ 3117 YouTube (문제 보기)

슬라이딩 윈도우(Sliding Window)

BOJ 2096 내려가기 (문제 보기)

AOJ SUSHI 회전초밥 (문제 보기)

행렬 곱셈을 이용한 고속 DP

BOJ 11444 피보나치 수6 (문제 보기)

BOJ 13328 Message Passing (문제 보기)

BOJ 1533 길의 개수 (문제 보기)

참고 자료

프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략, 구종만
Competive Programming 3, Steven Halim
http://www.geeksforgeeks.org/dynamic-programming/
http://codeforces.com/blog/entry/325

No Silver Bullet