그래프 탐색(Graph Search)

• 깊이 우선 탐색(Depth First Search, DFS)
• 너비 우선 탐색(Breadth First Search, BFS)
• 컴포넌트(Components) 찾기
• 위상 정렬(Topological Sort)
• 이분 그래프 검사하기(Bipartite Graph Checking)
• 사이클 찾기(Cycle Detection)
• 오일러 서킷(Eulerian Circuit) 찾기
• DFS 스패닝 트리(DFS Spanning Tree)
• 단절점(Articulation Points, Cut Vertices) 찾기
• 단절선(Bridges) 찾기
• 강결합 컴포넌트(Strongly Connected Components) 찾기
  • 타잔 알고리즘(Targan algorithm)
  • 코사라주 알고리즘 (Kosaraju’s algorithm)
  • 2-SAT 문제
• 연습 문제
• 참고 자료

깊이 우선 탐색(Depth First Search, DFS)

그래프의 모든 정점을 탐색하는 방법중 하나인 깊이 우선 탐색(이하 DFS)은 시작 정점부터 방문하여 현재 방문중인 정점 u에서 아직 방문하지 않은 정점 v로 향하는 간선이 존재한다면 그 간선을 타고 정점 v를 방문한다. 이 과정에서 더 이상 갈 곳이 없는 정점에 도달하면, 이 정점 이전에 마지막으로 방문했던 정점으로 돌아가 이와 같은 과정을 반복하는 탐색 알고리즘이다. 시간복잡도는 \(O(V+E)\)이다.

vector<int> adj[MAX_V];
vector<bool> visited[MAX_V]; // initially set all false

void dfs(int u) {
  visited[u] = true;
  cout << "visit vertex " << u << endl;
  for (int v: adj[u]) {
    if (!visited[v]) {
      dfs(v);
    }
  }
}

너비 우선 탐색(Breadth First Search, BFS)

또다른 그래프 탐색 방법중 하나인 너비 우선 탐색(이하 BFS)은 시작 정점에서부터 거리가 가까운 정점들부터 방문해나간다. BFS는 보통 그래프에서 최단 경로 문제를 풀때 많이 사용된다. 시간복잡도는 \(O(V+E)\)이다.

int V;
vector<int> adj[MAX_V];

void bfs(int source) {
  vector<int> dist(V, INF);
  dist[source] = 0;
  cout << "visit vertex 0 (Layered 0)" << endl;;
  queue<int> q;
  q.push(source);
  while (!q.empty()) {
    int u = q.front(); q.pop();
    for (int v : adj[u]) {
      if (dist[v] == INF) {
        dist[v] = dist[u] + 1;
        cout << "visit vertex " << v << " (Layered " << dist[v] << ")" << endl;
        q.push(v);
      }
    }
  }
}

컴포넌트(Components) 찾기

그래프에서 컴포넌트(connected component)란 다음 두 가지 특성을 만족하는 정점의 부분 집합이다.

• 부분 집합의 임의의 두 점 사이에는 경로(path)가 존재해야 한다.
• 부분 집합내의 임의의 정점 u와 부분 집합에 포함되지 않은 정점 v 사이에 경로가 존재해서는 안된다. (가능한 최대 부분 집합이어야 한다는 것)

무방향 그래프에서 컴포넌트들은 다음과 같이 DFS로 쉽게 찾아낼 수 있다.

int V;
vector<int> adj[MAX_V];
bool visited[MAX_V];

void dfs(int u) {
  visited[u] = true;
  cout << u << ' ';
  for (int v : adj[u])
    if (!visited[v])
      dfs(v);
}
void find_connected_components() {
  int cnt = 0;
  for (int i = 0; i < V; i++) {
    if (!visited[i]) { // visited[]: initially all false
      cout << "Connected Component " << cnt++ << ": ";
      dfs(i);
      cout << "\n";
    }
  }
}

위상 정렬(Topological Sort)

위상 정렬은 방향 그래프의 정점들을 정점들 사이의 간선 방향을 거스르지 않도록 나열하는 것으로 의존성이 있는 작업들을 목록이 있을 때, 어떤 순서로 작업을 해야 하는지 계산하는데 사용한다.

DAG(Directed Asyclic Graph)에서는 다음과 같이 DFS를 응용하여 위상 정렬을 할 수 있다. (사이클이 존재하는 방향 그래프에서는 위상 정렬을 할 수 없다)

int V;
vector<int> adj[MAX_V];
vector<int> order;
bool visited[MAX_V];

void dfs(int u) {
  visited[u] = true;
  for (int v : adj[u]) {
    if (!visited[v]) {
      dfs(v);
    }
  }
  order.push_back(u);
}
void topological_sort() {
  for (int i = 0; i < V; i++)
    if (!visited[i])
      dfs(i);
  reverse(order.begin(), order.end());
  cout << "order: ";
  for (int i = 0; i < order.size(); i++)
    cout << order[i] << ' ';
  cout << endl;
}

이분 그래프 검사하기(Bipartite Graph Checking)

이분 그래프란 다음 두 가지 특성을 만족하는 특수 그래프를 말한다.

• 그래프의 모든 정점들을 두 개의 상호 배타적 집합 A, B로 분할할 수 있다.
• 이때, 그래프의 모든 간선은 A의 정점과 B의 정점을 잇는 형태여야만 한다. (즉, A내의 어느 두 정점도 간선으로 연결되어 있지 않다. B도 마찬가지)

이분 그래프인지 검사하는 방법 또한 DFS로 쉽게 구현 가능하다. 서로 인접한 두 정점을 다른 색으로 칠해가는데 인접한 두 정점의 색이 같아지는 상황이 발생하면 이분 그래프가 아님을 확인할 수 있다.

int V;
vector<int> adj[MAX_V];
int color[MAX_V];

bool set_color(int u, int u_color) {
  color[u] = u_color;
  for (int v : adj[u]) {
    if (color[v] == INF && !set_color(v, 1 - color[u]))
      return false;
    else if (color[v] == color[u])
      return false;
  }
  return true;
}
bool is_bipartite() {
  for (int i = 0; i < V; i++)
    color[i] = INF;
  for (int i = 0; i < V; i++)
    if (color[i] == INF && !set_color(i, 0))
      return false;
  return true;
}

사이클 찾기(Cycle Detection)

추가 예정…

사이클과 관련된 그래프 특성

• 모든 정점의 나가는 간선의 차수가 1인 경우, 각각의 컴포넌트들은 최대 1개의 cycle을 갖는다.
• 무방향 그래프가 주어졌을 때, 이 그래프에 홀수 길이의 사이클이 존재하지 않는다는 말은 주어진 그래프가 이분 그래프라는 말과 동치다.

오일러 서킷(Eulerian Circuit) 찾기

추가 예정…

DFS 스패닝 트리(DFS Spanning Tree)

그래프의 단절점, 단절선, 강결합 컴포넌트를 찾는 알고리즘등과 같이 DFS를 응용하여 문제를 해결하려고 할 때, 알아두면 도움이 되는 개념이 있다. DFS 스패닝 트리와 그에 따른 간선 분류다. 어떤 연결된 그래프에 DFS를 수행할 때 탐색이 따라가는 간선들을 모아보면 트리 형태를 이루는 것을 알 수 있다. 이를 DFS 스패닝 트리라고 하는데 이러한 DFS 스패닝 트리를 생성하고 나면 그래프의 모든 간선을 다음과 같이 네 가지 중 하나로 분류할 수 있다.

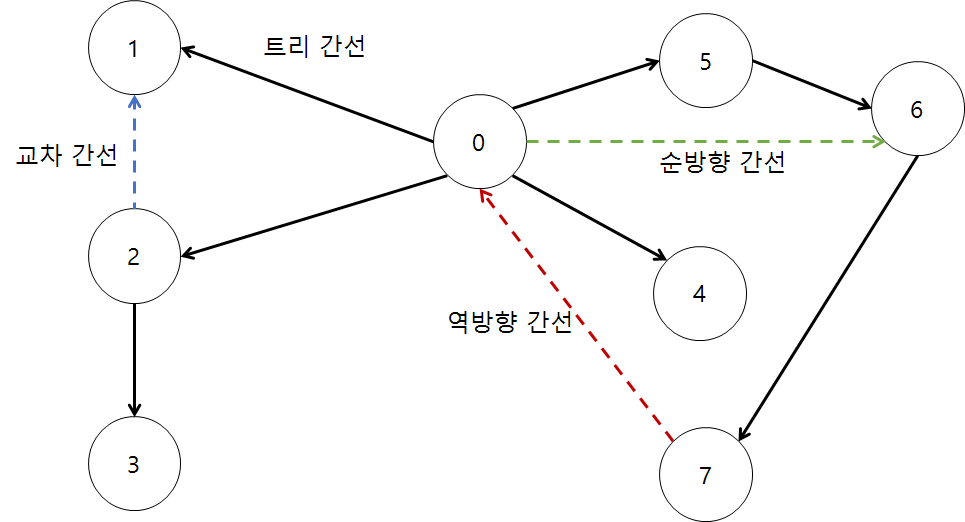
• 트리 간선(tree edge): 스패닝 트리에 포함된 간선
• 순방향 간선(forward edge): 스패닝 트리를 구성하는 트리 간선은 아니지만, 스패닝 트리의 선조에서 자손으로 연결되는 간선
• 역방향 간선(back edge): 스패닝 트리의 자손에서 선조로 연결되는 간선 (방향 그래프에서는 순방향 간선과 구분이 없다)
• 교차 간선(cross edge): 트리에서 선조와 자손 관계가 아닌 정점들 간에 연결된 간선 (방향 그래프에서만 존재)

위에서 분류한 대로 방향 그래프의 간선을 구분하는 것은 DFS를 수행하는 동안 처리할 수 있다. 현재 정점 u에 방문 중일 때, 인접한 정점 v와의 간선을 어떻게 분류할지를 고민하면 된다.

만약 정점 v를 아직 방문하지 않았다면, 다음에 v를 방문하므로 간선 (u, v)는 트리 간선이 된다. 그런데 v를 이미 방문한 경우 순방향, 역방향, 교차 간선 중 하나가 된다. 이 세 가지를 다시 구분해야 한다.

순방향의 간선이 역방향, 교차 간선과 구분되는 것이 하나 있다. 현재 정점 u보다 나중에 방문된 정점 v와의 간선이라는 것이다. 따라서 각 정점의 방문 순서(시간)를 저장해두면 구분할 수 있다.

역방향 간선과 교차 간선은 방문 순서로 구분할 수는 없다. 둘다 현재 정점 u보다 먼저 방문된 정점 v와의 간선이기 때문이다. 이 둘의 차이는 쉽게 생각하면 시작 정점을 루트로 하는 DFS 스패닝 트리에서 정점 v가 정점 u의 조상 노드(부모 노드 포함)인지 확인하는 것이다. 이는 v에서의 탐색이 종료된 상태인지를 확인하면 된다. 만약 v에서의 탐색이 종료하지 않았다면 역방향 간선, 종료했다면 교차 간선이라고 판단할 수 있다.

int V;
vector<int> adj[MAX_V];
int discovered[MAX_V]; // initially set all -1
bool finished[MAX_V];
int counter = 0;

void dfs_spanning_tree(int u) { // in directed graph
  discovered[u] = counter++;
  for (int v : adj[u]) {
    cout << "edge(" << u << ", " << v << ") is a ";
    if (discovered[v] == -1) {
      cout << "tree edge.\n";
      dfs_spanning_tree(v);
    }
    else if (discovered[u] < discovered[v])
      cout << "forward edge.\n";
    else if (!finished[v])
      cout << "back edge.\n";
    else
      cout << "cross edge.\n";
  }
  finished[u] = true;
}

단절점(Articulation Points, Cut Vertices) 찾기

무방향 그래프에서 정점 u와 u와 연결된 간선들을 지웠을 때, u가 속해있는 컴포넌트가 두 개 이상으로 나뉘어질 때, 이 정점 u를 단절점(Cur Vertex 또는 Articulation Point)라고 한다. 이러한 단절점을 찾는 가장 간단한 방법은 어떤 정점을 지운 후, 컴포넌트의 개수가 증가했는지 확인하는 것으로 총 \(V\)번의 DFS를 수행 되지만, DFS 스패닝 트리를 관찰하면 보다 효율적으로 단절점을 찾을 수 있다. 임의의 정점으로부터 DFS를 수행하여 얻은 DFS 스패닝 트리가 아래와 같다고 하자.

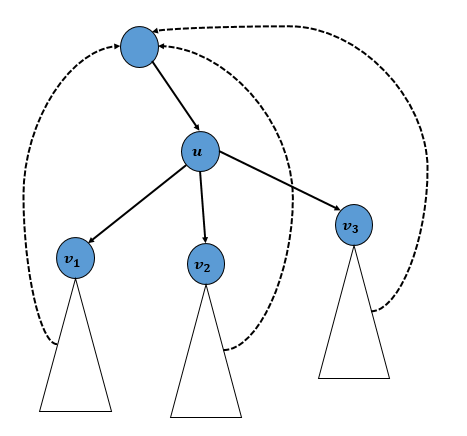
\(u\)의 자식 노드가 \(v_1, v_2, v_2\)이고, 이 \(v_1, v_2, v_3\) 각각을 루트로 하는 서브 트리가 형성되었다고 하자. 이때, 각각의 서브 트리와 \(u\)의 조상 노드가 모두 연결되어 있다면, (즉 역방향 간선이 존재하면) \(u\)를 없애도 컴포넌트가 나뉘어지지 않는다. 반대로 하나의 서브 트리라도 \(u\)의 선조들로 향하는 역방향 간선이 존재하지 않으면, \(u\)는 절단점이 된다.

단, 위의 상황은 \(u\)가 DFS 스패닝 트리의 루트 이외의 정점일 때 성립한다. 루트 정점일 때는 따로 처리해주어야 하는데, 루트 정점의 트리 간선이 1개라면 이 정점을 제거해도 그래프의 컴포넌트가 증가하지 않는다. 반대로 루트 정점은 트리 간선의 개수가 2개 이상이면 무조건 단절점이 된다.

아래와 같이 단절점을 찾는 코드를 구현할 수 있는데, 여기서 low[v]는 각 \(v\)의 서브 트리내의 정점에서 v의 부모인 u와의 간선을 제외한 역방향 간선을 통해 도달할 수 있는 방문 시간이 가장 빠른 정점을 기록한다. (여기서 방문 시간이 가장 빠른 정점이 최상위 정점이 된다. 그리고 방문 시간은 각 정점마다 다르기 때문에 각 정점을 구별할 수 있다.) low[v]를 알고 있다면 \(v\)와 그 부모 \(u\)사이의 간선을 제거했을 때, \(u\)의 조상과의 연결이 끊키는지 확인할 수 있다.

int V;
int counter; // time counter
int discovered[MAX_V]; // discovered[u]: time u visited
int low[MAX_V]; // Top vertex('s visit time) reachable
vector<int> adj[MAX_V];
bool cut_vertex[MAX_V];

void find_cut_vertices(int u, int parent = -1, bool root = true) {
  low[u] = discovered[u] = counter++;
  int children = 0; // for root
  for (int v : adj[u]) {
    if (discovered[v] < 0) {
      children++; // for root
      find_cut_vertices(v, u, false);
      if (low[v] >= discovered[u]) {
        cut_vertex[u] = true;
      }
      low[u] = min(low[u], low[v]);
    } else if (v != parent) {
      low[u] = min(low[u], discovered[v]);
    }
  }
  if (root) { // for root
    cut_vertex[u] = children > 1 ? true : false;
  }
}

단절선(Bridges) 찾기

단절점과 유사하게 제거했을 때 컴포넌트의 개수를 증가시키는 간선을 단절점 또는 다리(bridge)라고 부른다. 이 단절선 역시 단절점을 구하는 것과 유사하게 구할 수 있다. DFS 중 현재 정점이 \(u\)이고, \(u\)와 인접한 정점이자 DFS 스패닝 트리상의 자식 정점인 \(v\)와의 간선 \((u, v)\)이 단절선이 될 수 있는 경우를 고려해보자. DFS 스패닝 트리상 \(v\)를 루트로 하는 서브 트리가 생성될 것이다. 이 서브 트리에서 \((u, v)\)를 제외한 간선을 통해 정점 \(v\)의 조상 노드로 향하는 역방향 간선이 존재하지 않으면, 간선 \((u, v)\)를 지웠을 때 이 서브 트리는 분리된다. 따라서 이러한 간선 \((u, v)\)가 단절선이 된다. 구현 코드는 단절점 코드와 상당히 유사하다.

int V, counter, discovered[MAX_V], low[MAX_V]; // initially set all -1
vector<int> adj[MAX_V];
vector<pair<int, int>> bridges;

void find_bridges(int u, int parent = -1) {
  low[u] = discovered[u] = counter++;
  for (int v : adj[u]) {
    if (discovered[v] < 0) {
      find_bridges(v, u);
      if (low[v] > discovered[u]) {
        bridges.push_back(make_pair(min(u, v), max(u, v)));
      }
      low[u] = min(low[u], low[v]);
    } else if (v != parent) {
      low[u] = min(low[u], discovered[v]);
    }
  }
}

강결합 컴포넌트(Strongly Connected Components) 찾기

방향 그래프에서 정의되는 개념중에 강결합 요소가 있다. 다음 조건들을 만족하는 정점들의 집합을 강결합 컴포넌트(Strongly Connected Components, 줄여서 SCC)라고 부른다.

1. SCC내의 임의의 두 정점 \(u, v\) 사이에 \(u\) -> \(v\) 경로, \(v\) -> \(u\) 경로가 모두 존재한다.
2. 서로 다른 SCC에 속하는 임의의 두 정점 \(u, v\)에 대해 \(u\) -> \(v\) 경로, \(v\) -> \(u\) 경로가 모두 존재할 수 없다. (= SCC는 가능한 최대 집합이어야 한다)

방향 그래프에서 각각의 강결합 컴포넌트를 구분하는 대표적인 알고리즘으로는 타잔 알고리즘과 코사라주 알고리즘이 있다.

타잔 알고리즘(Targan algorithm)

타잔 알고리즘은 DFS를 통해 생성되는 DFS 스패닝 트리와 그에 따른 간선 분류를 통해서 방향 그래프의 SCC를 구한다. 방향 그래프의 DFS 스패닝 트리를 관찰해보면 알 수 있는 사실이 몇 가지 있다. 모든 SCC에 대해 SCC의 한 정점을 루트로 하고, SCC를 이루는 정점들은 모두 포함하는 서브 트리가 DFS 스패닝 트리에 존재한다는 것이다. 이를 만족하지 않는 정점이 있다고 가정하면 금방 모순이 된다는 것을 확인할 수 있다.

그러므로 DFS를 수행하면서 각 정점 \(u\)에 대해 정점 \(u\)가 자신이 속해 있는 SCC를 포함하는 서브 트리의 루트가 될 수 있는지를 판단하면 된다. 정점 \(u\)가 서브 트리의 루트가 될 수 있다고 판단되면 자신을 포함하여 서브 트리상에서 아직 SCC로 묶이지 않은 정점들과 하나의 SCC를 이룰 수 있게 된다. \(u\)를 루트로 하는 서브 트리에서 \(u\)와 같은 SCC에 속할 수 없는 정점들은 DFS의 특성상 이미 \(u\)를 루트로 하는 서브 트리 내부의 또다른 서브 트리들은 형성하면서 각각의 SCC로 배정되어 있기 때문에 가능한 일이다.

각 정점 \(u\)에 대해 정점 \(u\)가 자신이 속해있는 SCC를 포함하는 서브 트리의 루트인지 확인하는 것은 단절점, 단절선을 구할 때와 유사하게 low[u]를 통해 알 수 있다. low[u]가 \(u\)의 방문 시간과 일치한다면 루트가 된다. 무방향 그래프에서 정의된 단절점, 단절선과 다르게 SCC는 방향 그래프에서 정의되는 개념이기 때문에 low[u]를 구할 때, 교차 간선에 유의해야 한다. 현재 정점이 \(u\)일 때 low[u]에 대한 정보는 다음과 같이 얻을 수 있다.

• 일단, low[u] <= discovered[u] 인 것은 당연하다.
• 트리 간선을 타고가 만나는 정점 v와 v를 루트로 하는 서브 트리내의 정점은 u를 루트로 하느 서브 트리내의 정점에 모두 포함되므로 low[u] <= low[v] 이다.
• 순방향 간선을 타고가 만나는 정점 v에서 얻을 수 있는 정보는 트리 간선을 통해 얻을 수 있으므로 무시해도 된다.
• 역방향 간선을 타고가 만나는 정점 v는 u의 조상이므로 low[u] <= discovered[v] 가 된다.
• 교차 간선을 타고가 만나는 정점 v는 u의 조상도 아니고, 서브 트리내의 정점도 아니다. 하지만 v가 아직 별도의 SCC로 묶여있지 않은 상황이면 u와 v가 같은 SCC로 묶이게 되므로, 이 경우 low[u] <= discovered[v] 가 된다.

int V;
vector<int> adj[MAX_V];
vector<int> discovered, low, scc_id; // initially set all -1
stack<int> s;
int counter, scc_counter; // initially set all 0

void targan_scc(int u) {
  low[u] = discovered[u] = counter++;
  s.push(u);
  for (int v : adj[u]) {
    if (discovered[v] < 0) {
      targan_scc(v);
      low[u] = min(low[u], low[v]);
    } else if (scc_id[v] < 0) {
      low[u] = min(low[u], discovered[v]);
    }
  }
  if (low[u] == discovered[u]) {
    while (true) {
      int v = s.top(); s.pop();
      scc_id[v] = scc_counter;
      if (u == v) break;
    }
    scc_counter++;
  }
}

코사라주 알고리즘 (Kosaraju’s algorithm)

코사라주 알고리즘(Kosaraju’s algorithm)은 두 번의 DFS (정방향 DFS 한 번, 역방향 DFS 한 번)로 방향 그래프의 강한 컴포넌트들을 구분한다.

int V;
vector<int> adj[MAX_V], radj[MAX_V], sid, order;
vector<bool> visited;

void dfs(int u) {
  visited[u] = true;
  for (int v : adj[u]) {
    if (!visited[v]) {
      dfs(v);
    }
  }
  order.push_back(u);
}
void rdfs(int u, int id) {
  sid[u] = id;
  for (int v : radj[u]) {
    if (sid[v] == -1) {
      rdfs(v, id);
    }
  }
}
int kosaraju_scc() {
  visited.assign(V, false);
  for (int u = 0; u < V; u++) {
    if (!visited[u]) {
      dfs(u);
    }
  }
  reverse(order.begin(), order.end());
  int id = 0;
  sid.assign(V, -1);
  for (int u : order)  {
    if (sid[u] == -1) {
      rdfs(u, id++);
    }
  }
  return id;
}

2-SAT 문제

추가 예정…

연습 문제

BOJ 2331 반복수열 (문제 보기)

BOJ 2487 섞기 수열 (문제 보기)

BOJ 2234 성곽 (문제 보기)

BOJ 9466 텀 프로젝트 (문제 보기)

BOJ 2617 구슬 찾기 (문제 보기)

BOJ 2178 미로 탐색 (문제 보기)

BOJ 13903 출근 (문제 보기)

BOJ 2146 다리 만들기 (문제 보기)

BOJ 1697 숨바꼭질 (문제 보기)

BOJ 12851 숨바꼭질 2 (문제 보기)

BOJ 2206 벽 부수고 이동하기 (문제 보기)

BOJ 1734 교통 체계 (문제 보기)

참고 자료

• 프로그래밍 대회에서 배우는 알고리즘 문제해결전략, 구종만
• Competive Programming 3, Steven Halim