네트워크 유량(Network Flow)
최대 유량(Maximum Flow)
유량 네트워크(Flow Network)
유량 네트워크란 각 간선에 용량(capacity)이라는 속성이 존재하는 방향 그래프를 말한다. 이 유량 네트워크는 다음과 같은 요소들을 가진다.
- 소스(source)- 유량 네트워크에서 모든 유량이 흘러나오는 정점
- 싱크(sink): 유량 네트워크에서 모든 유량이 최종적으로 도달하는 정점
- 용량(capacity): 간선에 최대한 흘릴 수 있는 유량의 양
- 유량(flow): 간선에 실제로 흐르는 유량의 양
- 잔여용량(residual capacity): ‘용량 - 유량’, 간선에 흘릴 수 있는 유량의 양
최대 유량이란?
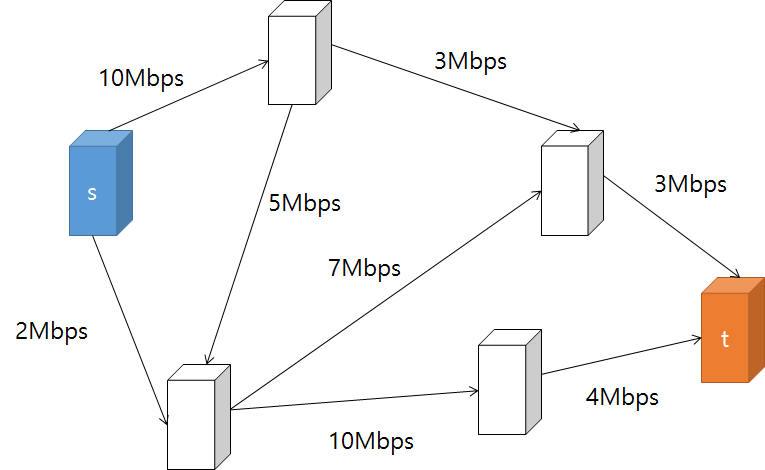
이러한 유량 네트워크에서 소스(source)에서 싱크(sink)로 얼마나 많은 유량(flow)을 보낼 수 있는지, 즉 최대 유량을 계산하는 문제를 네트워크 유량 문제라고 한다. 예를 들어, 아래 그림과 같이 여러 컴퓨터들이 각기 다른 대역폭을 가진 케이블들로 연결된 네트워크에서 컴퓨터 s에서 t로 데이터를 보낼 때, 1초간 보낼 수 있는 최대 데이터 양을 구하는 문제가 대표적인 네트워크 유량 문제다.
포드-풀커슨 알고리즘(Ford-Fulkerson Algorithm)
유량 네트워크에서 최대 유량을 찾는 비교적 간단한 방법으로 포드-풀커순 알고리즘이 알려져 있다. s에서 t로 유량을 보낼 수 있는 경로를 찾아 해당 경로를 통해 보낼 수 있는 유량을 최대한 보내기를 반복하는 것이 이 알고리즘의 핵심이다. 여기서 s에서 t로 유량을 보내는 경로를 증가 경로(augmenting path)라고 부른다. 이 방법의 대략적인 의사코드는 다음과 같다.
mf = 0
while (s에서 t로 가는 증가 경로가 존재) {
1. 증가 경로(s -> a -> b -> ... -> t)에서 최소 잔여용량 f를 찾는다.
2. 증가 경로의 모든 정방향 정점쌍 (a, b)에 대하여 용량(a, b)를 f만큼 감소시킨다.
3. 증가 경로의 모든 역방향 정점쌍 (b, a)에 대하여 용량(b, a)를 f만큼 감소시킨다.
4. mf += f
}
return mf // 최대 유량
위의 코드를 보면 느낄 수 있지만 포드-풀커슨 알고리즘은 증가 경로를 어떻게 찾을지부터 해서 구체적인 구현 방법은 제시하지 않느다(때문에 포드-풀커슨 기법이라고 부르기도 한다). 증가 경로는 그래프 탐색 알고리즘들(DFS, BFS)을 이용하여 구할 수 있다. 만약 최대 유량을 \(f\)라고 가정하고, 매번 찾은 증가 경로로 보낼 수 있는 유량이 1이라고 하면 증가 경로를 한 번 찾는데 \(O(E)\)가 걸리므로 이 포드-풀커슨 알고리즘의 시간복잡도는 \(O(fE)\)가 된다. 증가 경로를 어떻게 찾느냐에 따라 알고리즘의 속도가 향상될 수 있는데 만약 증가 경로를 DFS로 찾으면 매번 보낼 수 있는 유량이 1인 경로만 찾을 가능성도 있다. 하지만 BFS로 찾으면 이를 방지할 수 있다. 이 내용은 후술하는 알고리즘에서 설명하기로 한다.
에드몬드-카프 알고리즘(Edmonds-Karp Algorithm)
포드-풀커슨 알고리즘에서 제시한 방법을 보다 구체적으로 구현한 알고리즘이 에드몬드-카프 알고리즘이다. 이 알고리즘에서는 너비우선탐색(BFS)을 수행하여 최단 증가 경로를 구한 뒤 유량을 흘려주기를 반복한다.
매번 증가 경로를 통해 보낼줄 수 있는 유량을 최대한 흘려줄 때마다 최단 증가 경로의 길이는 유지되거나 증가한다. 하지만 매번 용량과 유량이 같아지는 포화 간선이 적어도 하나 생기게 된다. 이렇게 매번 유량을 흘릴때마다 포화간선은 늘어나고 \(O(E)\)내에 유량 그래프의 최단 증가 경로의 길이가 증가하거나 모든 경로가 막힐 것이다. 증가 경로의 길이는 최대 \(O(V)\)이므로 BFS를 \(O(VE)\)번 수행하면 모든 증가 경로를 찾을 수 있다는 얘기가 된다. 따라서 이 알고리즘의 총 시간복잡도는 \(min(O(VE^2), O(fE))\)가 되고 아래와 같이 구현할 수 있다.
struct Edge { int to, cap, flow; };
int V;
vector<int> adj[MAX_V];
vector<Edge> edges;
void add_edge(int from, int to, int cap) {
// 정방향 edge 번호(모두 홀수) + 1 = 역방향 edge 번호(모두 짝수)
adj[from].push_back(edges.size());
edges.push_back({ to, cap, 0 }); // 정방향
adj[to].push_back(edges.size());
edges.push_back({ from, 0, 0 }); // 역방향
}
int edmonds_karp(int s, int t) {
int mf = 0;
while (true) {
vector<int> parent(V, -1);
vector<int> edgeTo(V, -1);
queue<int> q;
q.push(s);
parent[s] = s;
while (!q.empty() && parent[t] < 0) {
int here = q.front(); q.pop();
for (int eid : adj[here]) {
Edge& e = edges[eid];
if (e.cap - e.flow > 0 && parent[e.to] < 0) {
q.push(e.to);
parent[e.to] = here;
edgeTo[e.to] = eid;
}
}
}
if (parent[t] < 0) break;
int f = INF;
for (int p = t; p != s; p = parent[p]) {
Edge& e = edges[edgeTo[p]];
f = min(f, e.cap - e.flow);
}
for (int p = t; p != s; p = parent[p]) {
Edge& fe = edges[edgeTo[p]];
Edge& re = edges[edgeTo[p] ^ 1];
fe.flow += f;
re.flow -= f;
}
mf += f;
}
return mf;
}
디닉 알고리즘(Dinic’s Algorithm)
Yefim Dinitz라는 사람에 의해 개발된 이 알고리즘은 최단 증가 경로를 이용한다는 점에서 에드몬드-카프 알고리즘과 유사한 알고리즘이다. 시간복잡도는 \(min(O(fE), O(V^2E))\)으로 대개 에드몬드-카프보다 빨리 동작한다.
에드몬드-카프 알고리즘에서는 매번 BFS로 최단 증가 경로를 찾고 유량을 흘리는 작업을 반복하지만, 디닉 알고리즘에서는 최단 증가 경로의 길이가 커지지 않는 이상 다시 BFS를 수행하지 않는다. 최단 증가 경로의 길이가 커졌을 경우에만 다시 BFS로 최단 증가 경로를 찾기 위한 준비를 한다(에드몬드에서는 BFS로 직접 증가 경로를 찾는다는 것을 기억하자). 이를 설명하기 위해서 준위 그래프(level graph)란 개념을 사용한다. 준위 그래프(level graph)는 유량 그래프 내의 모든 정점 v에 대해 source로부터 잔여 용량이 남아 있는 간선을 따라 도달할 수 있는 최단 거리 dist[v]를 매겨놓은 그래프를 말한다.
디닉 알고리즘에서는 BFS로 준위 그래프를 만들고, 이 그래프에서 증가 경로를 찾는다. 이때 증가 경로는 경로를 이루는 모든 간선 (u, v)에 대해 잔여 용량이 남아 있고, dist[u] + 1 == dist[v]가 만족되어야 한다. 그러면 이 경로는 당연히 최단 증가 경로가 된다. 여기에 유량을 흘려주고, 이 그래프에서 대해서 다시 최단 증가 경로를 찾고 유량 흘려주기를 반복한다. 더 이상 증가 경로를 찾을 수 없는 순간이 온다. 이때 BFS로 다시 준위 그래프를 갱신해준뒤 이전 과정을 반복한다. BFS로 준위 그래프를 만들었는데 source에서 sink로 도달할 수 없다면 더 이상 흘릴 수 있는 유량이 없으므로 알고리즘은 종료한다.
왜 이 알고리즘이 \(O(V^2E)\)인지 궁금할 것이다. 이 알고리즘에서 준위 그래프를 찾는 과정은 BFS로 \(O(E)\)의 시간이 소요된다. 최단 증가 경로의 길이는 \(O(V)\) 이기 때문에 준위 그래프는 최대 \(O(V)\)번 만들 것이다(여기까지는 에드몬드-카프 알고리즘에서 설명한 내용과 크게 다르지 않다). 그리고 어떤 준위 그래프에서 증가 경로를 찾고 흘려주기를 반복하는 과정에는 \(O(VE)\)의 시간이 소요된다. 이를 설명하기 위해 어떤 준위 그래프에서 증가 경로 하나를 찾았다고 하자. 이 증가 경로를 통해 유량을 흘릴 것이다. 그러면 이 준위 그래프에는 증가 경로가 더 남아있을수도 있고 그렇지 않을 수도 있다. 더 남아 있다면 경로를 통해 유량을 흘릴 것이다. 이 준위 그래프에는 \(O(E)\)개의 증가 경로가 있을 수 있을수 있고(앞서 에드몬드-카프 알고리즘에서 포화 간선으로 설명한 부분) , 증가 경로의 길이는 \(O(V)\)이므로 이 준위 그래프에서 찾을 수 있는 모든 증가 경로의 길이는 \(O(VE)\)이다. 고로 이 준위 그래프내의 모든 증가 경로로 유량을 흘려주는데에는 \(O(VE)\)의 시간이 소요된다. 유량을 흘려주는데에는 \(O(VE)\)의 시간이 걸리는 것은 명확하다. 하지만 그러한 모든 증가 경로를 찾는데에는 당연히 좀 더 시간이 걸리지 않을까라고 생각할 수도 있는데 구현을 잘하면 별차이 없이 모든 증가 경로를 찾는데에도 \(O(VE)\)의 시간이 소요되게 할 수 있다. 이 부분은 구현 코드를 보고 판단하는 것이 좋다. 아래의 구현에서 DFS로 준위 그래프의 증가 경로를 찾고, 유량을 흘려주는 부분을 잘보도록 하자. DFS의 각 단계에서 iter 배열 변수를 활용하여 유량을 흘려줄 수 없는 간선들은 한 번 조사한 후 다시 조사하지 않기 때문에 이 과정은 \(O(VE)\)가 된다.
struct Edge { int to, cap, rev; };
vector<Edge> adj[MAX_V];
int level[MAX_V];
int iter[MAX_V];
void add_edge(int from, int to, int cap) {
adj[from].push_back({ to, cap, adj[to].size() });
adj[to].push_back({ from, 0, adj[from].size() - 1 });
}
void bfs(int src) {
memset(level, -1, sizeof(level));
queue<int> q;
q.push(src);
level[src] = 0;
while (!q.empty()) {
int here = q.front(); q.pop();
for (Edge& e : adj[here]) {
if (e.cap > 0 && level[e.to] < 0) {
level[e.to] = level[here] + 1;
q.push(e.to);
}
}
}
}
int dfs(int here, int sink, int flow) {
if (here == sink) return flow;
for (int& i = iter[here]; i < adj[here].size(); i++) {
Edge& e = adj[here][i];
if (e.cap > 0 && level[here] < level[e.to]) {
int minFlow = dfs(e.to, sink, min(flow, e.cap));
if (minFlow > 0) {
e.cap -= minFlow;
adj[e.to][e.rev].cap += minFlow;
return minFlow;
}
}
}
return 0;
}
int dinic(int src, int sink) {
int mf = 0;
while (true) {
bfs(src);
if (level[sink] < 0) break;
memset(iter, 0, sizeof(iter));
int f = 0;
while ((f = dfs(src, sink, INF)) > 0)
mf += f;
}
return mf;
}
추가로 source와 sink에 연결된 간선들은 제외한 모든 간선이 단위 용량(unit capacity)으로 이루어진 유량 네트워크에서 디닉 알고리즘의 시간복잡도는 \(min(O(V^{1.5}E), O(\sqrt EE))\)라고 한다.
최소 컷 최대 유량 정리(Min-cut Max-flow Theorem)
그래프의 컷(cut)이란 그래프의 정점들을 두 개의 집합(disjoint set)으로 분할(partition)하는 것을 말한다. 보통 유량 네트워크의 컷은 소스와 싱크가 각각 다른 집합에 속하도록 그래프의 정점들을 분할하는 것을 말한다. 이때 소스가 속한 집합을 S, 싱크가 속한 집합을 T라고 하면 다음과 같이 여러 방식으로 유량 네트워크를 컷(cut) 할 수 있다. (그림에서 사용된 컷 S, T의 용량은 집합 S에서 T로 가는 간선들의 용량 합이다.)
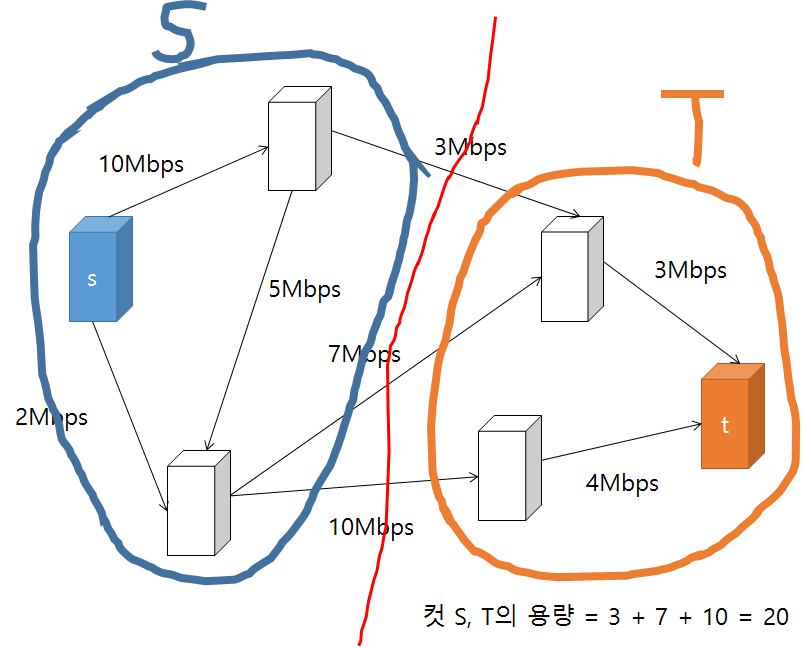
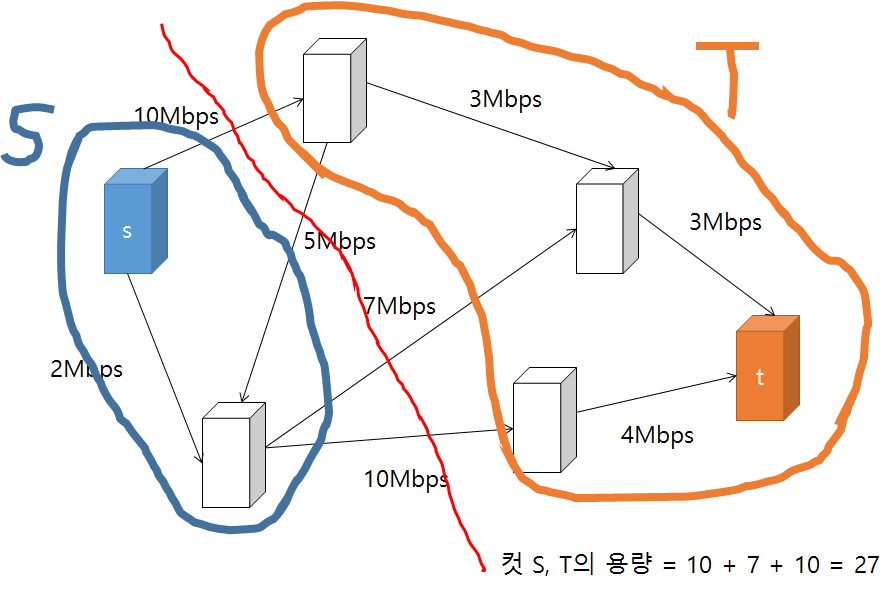
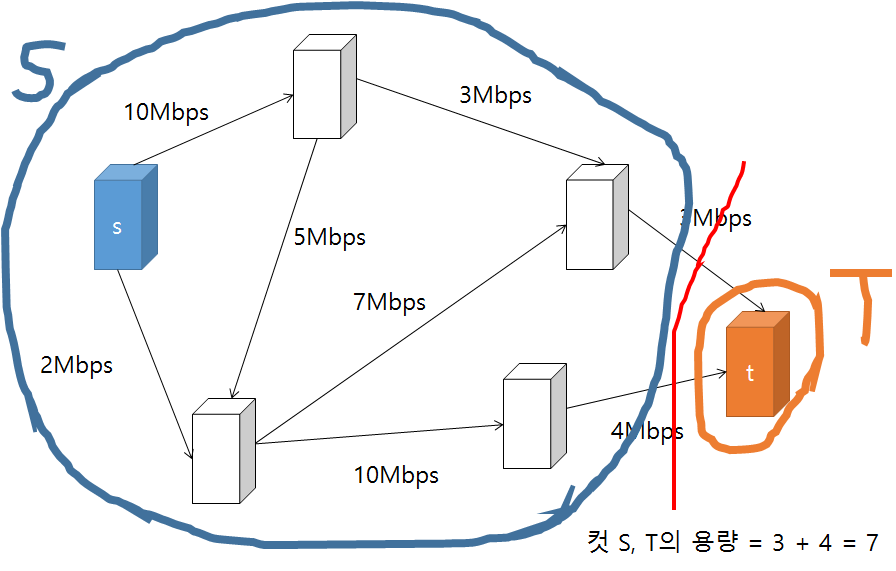
위와 같이 유량 네트워크를 S, T로 분할하는 여러 컷이 존재할 수 있는데 가장 용량이 작은 컷을 찾아내는 문제를 최소 컷 문제(min-cut problem)이라고 한다. 최소 컷 최대 유량 정리 에서는 유량 네트워크의 소스에서 싱크로 가는 최대 유량은 최소 컷의 비용(컷의 총 용량)과 같다고 설명한다.
왜 그런지 생각해보자. 일단 어떻게 네트워크를 컷 하던 해당 컷의 유량은 소스에서 싱크로 가는 최대 유량과 같을 것이다. 그리고 컷의 유량은 당연히 컷의 용량보다 작을 수 밖에 없으므로 최대 유량은 어떤 컷의 용량보다도 작거나 같다. 즉, 최대 유량은 최소 컷의 용량보다 작거나 같아야 한다.
이제 최대 유량이 최소 컷의 용량보다 작을 수 없다는 것을 확인하면 된다. 최소 컷의 용량보다 최대 유량 f가 작다고 가정해보자. 현재 f의 유량이 흐르고 있고 이것이 최대 유량이라면 가능한 모든 컷에 대해 ‘컷의 용량 = 컷의 유량’을 만족하는 컷이 적어도 하나 존재해야 한다. 컷의 유량은 f이고 최소 컷 > f 이므로 여기서 모순이 발생한다. 따라서 최대 유량은 최소 컷의 용량보다 작을 수 없다. 즉, 최대 유량과 최소 컷의 용량이 같다 얘기다.
최소 비용 최대 유량(Minimum Cost Maximum Flow)
최소 비용 최대 유량 문제는 유량 네트워크에 최대 유량을 흘릴 때, 최소 비용으로 흘려보내는 방법을 찾는 문제다. 이런 문제는 증가 경로를 찾을 때 최단 거리 알고리즘을 사용하여 찾은 뒤 유량을 흘려주면 풀 수 있다. 최대 유량 문제를 풀 때 역방향 간선을 따라 특정 유량을 감소하게 되면 음수 간선을 통해 이동하는 것이므로 음수 간선에서도 잘 동작하는 알고리즘을 사용해야 한다. 벨만-포드 알고리즘이나 SPFA를 사용하면 된다. 이 경우 시간복잡도는 \(O(V^2E^2)\)이 된다.
이분 매칭(Bipartite-Matching)
최대 유량 문제를 활용하여 해결할 수 있는 중요한 문제중 하나로 이분 그래프에서 이분 매칭을 찾는 것이 있다. 일단 이분 그래프와 이분 매칭이 무엇인지 설명한다.
이분 그래프(Bipartite Graph)
이분 그래프란 그래프의 모든 정점들을 두 개의 상호 배타적 집합 A, B로 분할(partition)할 수 있고, 모든 간선이 A의 정점과 B의 정점을 잇는 형태로 구성된 그래프를 말한다.
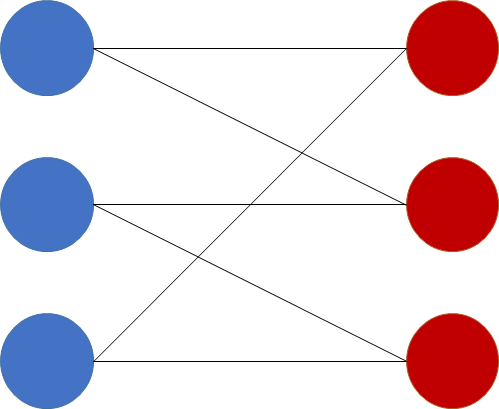
매칭 문제(Matching Problem)
그래프에서 매칭(mathing)이란 간선 집합 E에서 끝점을 공유하지 않는 간선의 집합 M (\(\subseteq\) E) 을 의미한다. 특히 가장 큰 매칭을 찾아내는 문제를 최대 매칭 문제(maximum matching)라고 한다. 일반적으로 ‘매칭 문제 = 최대 매칭 문제’라고 생각하면 된다.
프로그래밍 대회에서 일반적인 매칭 문제는 보통 나오지 않는다. 대신 좀더 단순한 형태의 그래프인 이분 그래프에서의 최대 매칭을 구하는 이분 매칭(bipartite matching) 문제가 자주 출제된다. 다음과 같은 문제가 대표적인 이분 매칭 문제이다.
N개의 컴퓨터에 M개의 작업을 하나씩 배정하려고 한다. 이때, 각 컴퓨터가 수행할 수 있는 작업의 목록은 모두 다르다. 각 컴퓨터가 수행할 수 있는 작업의 목록이 주어질 때, 최대로 몇 개의 일을 수행할 수 있는지를 구하여라.
이분 매칭을 최대 유량 문제로 바꿔 풀기
이분 매칭 문제는 최대 유량 문제로 바꾸면 쉽게 해결이 가능하다. 소스와 싱크를 추가하고 두 정점 집합 A, B와 용량이 1인 간선들을 이어주면 유량 네트워크가 완성되고, 이분 매칭 문제는 유량 네트워크의 최대 유량을 구하는 문제와 같아진다.
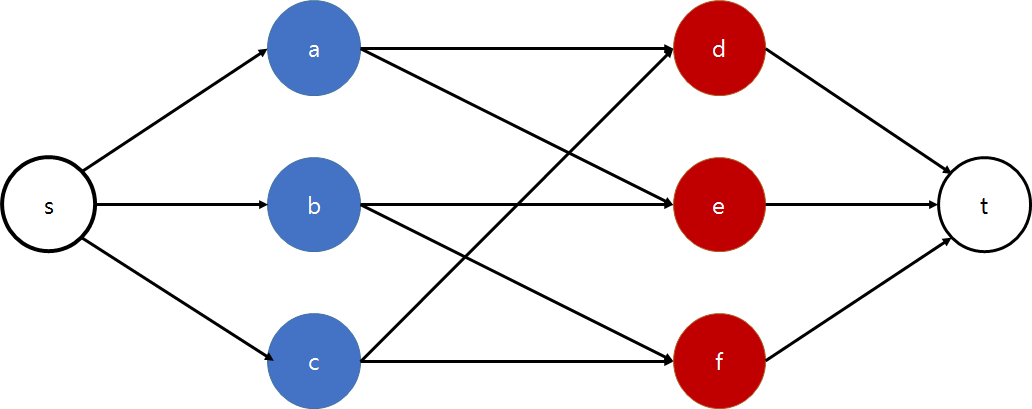
이분 매칭을 풀기 위해 이분 그래프에 소스와 싱크를 연결하여 유량 네트워크를 만든 후, 포드-풀커슨 알고리즘으로 구현할 수도 있지만, 이분매칭은 보다 단순한 형태이기 때문에 아래와 같이 보다 간결하게 코드를 작성할 수도 있다.
int V;
vector<int> adj[MAX_V];
int match[MAX_V];
bool used[MAX_V];
bool dfs(int a) {
if (used[a]) return false;
used[v] = true;
for (int b : adj[a]) {
if (match[b] < 0 || dfs(match[b])) {
match[b] = a;
match[a] = b;
return true;
}
}
return false;
}
int bipartite_matching() {
int matching = 0;
memset(match, -1, sizeof(match));
for (int a = 0; a < V; a++) {
memset(used, false, sizeof(used));
if (dfs(a)) {
++matching;
}
}
return matching
}
최대 독립 집합, 최소 정점 덮개
그래프의 독립 집합(independent set)이란 정점 집합 V에서 서로 인접하지 않는 정점 집합 I (\(\subseteq\) V)을 의미한다. 특히 정점의 수가 최대인 독립 집합을 최대 독립 집합(maximum indentpent set)이라고 한다.
그래프의 정점 덮개(vertex cover)는 정점 집합 V에서 모든 간선을 커버하는 정점 집합 S (\(\subseteq\) V)을 의미한다(보다 자세하게는 그래프의 모든 간선에 대해 각 간선 (u, v) \(\in\) E의 끝 정점 u, v 중 적어도 하나를 포함하는 정점 집합을 의미한다). 이 중 최소 정점 수를 가진 집합을 최소 정점 덮개(minumum vertex cover)라 부른다. 유사하게 간선 덮개(edge cover)는 정점 집합 E에서 모든 정점을 커버하는 간선 집합 F (\(\subseteq\) E)이고, 그 중 최소의 간선 수를 가진 집합을 최소 간선 덮개라 한다.
위의 용어들과 관련해서 다음 사실들을 알아두면 여러 문제들을 이분 매칭으로 모델링할 때 도움이 된다.
- 연결된 그래프 \(G=(V, E)\)에서
|최대 독립 집합| + |최소 정점 덮개| = |V|이다. - 연결된 그래프 \(G=(V, E)\)에서
|최대 매칭| + |최소 간선 덮개| = |V|이다. - 이분 그래프에서
|최대 매칭| = |최소 정점 덮개|이다.
연습 문제
최대 유량
BOJ 2316 도시 왕복하기 (문제 보기)
1번 도시에서 2번 도시로 갈 수 있는 경로의 수를 세는 문제이다. 이때 각 도시는 오직 한 경로에만 포함될 수 있으므로 각 도시를 두 개의 정점 in과 out으로 나눈 뒤 in -> out으로 용량 1인 간선을 그어준다(단, 1번 도시와 2번 도시 방문 횟수 제한이 없으므로 in -> out 용량을 무한으로 설정). 도시 x에서 도시 y 사이의 길이 존재하면 x_out -> y_in, y_out -> x_in으로 용량 1인 간선을 각각 그어주면 된다. 이러면 1번 도시를 source, 2번 도시를 sink로 하는 유량 네트워크가 완성되고 이 네트워크의 최대 유량이 곧 경로의 수가 된다.
BOJ 5651 완전 중요한 간선 (문제 보기)
유량 네트워크에서 최대한 유량을 흘린 상황을 상상해보자. 이 순간에 잔여 용량이 남아 있는 간선, 즉 ‘용량 - 유량’ 이 0보다 크다면 이 간선의 용량을 1 줄인다고 하더라도 최대 유량이 변하지 않을 것이라는 것은 당연하다. 그렇다면 잔여 용량이 남아 있지 않은 간선 (u, v)에 대해서 생각해보자. 이 순간에 u에서 v로 흐를 수 있는 경로 s가 존재한다면 간선 (u, v)의 용량을 1 줄이더라도 s를 통해 유량 1이 채워져 네트워크의 최대 유량은 변함이 없을 것이다. 반면에 u에서 v로 흐를 수 있는 경로가 존재하지 않다면 간선 (u, v)의 용량을 줄였을때 v에서 sink로 가는 유량이 1 줄어들기 때문에 최대 유량이 1 감소할 것이다.
BOJ 11495 격자 0 만들기 (문제 보기)
BOJ 1658 돼지 잡기 (문제 보기)
BOJ 10319 좀비 아포칼립스 (문제 보기)
BOJ 3666 리스크 (문제 보기)
MCMF
BOJ 11408 열혈강호 5 (문제 보기)
BOJ 11409 열혈강호 6 (문제 보기)
이분 매칭
BOJ 9576 책 나눠주기 (문제 보기)
BOJ 11376 열혈강호 2 (문제 보기)
BOJ 11377 열혈강호 3 (문제 보기)
BOJ 1017 소수 쌍 (문제 보기)
BOJ 1014 컨닝 (문제 보기)
BOJ 2570 비숍2 (문제 보기)
BOJ 9577 토렌트 (문제 보기)
참고 자료
- 프로그래밍 대회에서 배우는 알고리즘 문제해결전략, 구종만
- 프로그래밍 콘테스트 챌린징, Takuya Akiba, Yoichi Iwata, Mastoshi Kitagawa
- Competive Programming 3, Steven Halim
- http://blog.naver.com/PostView.nhn?blogId=kks227&logNo=220804885235
- http://koosaga.com/18
- http://koosaga.com/133