구간 트리(Segment Tree)

23 Aug 2017

구간 트리란?

구간 트리(segment tree)는 일차원 배열의 특정 구간에 대한 질문(query)을 빠르게 답하는데 사용할 수 있는 자료 구조이다. 예를 들어 배열 A = { 1, 3, 4, 2, 3, 1, 7 }와 같은 배열에서 구간 a[2..5]의 합을 빠르게 구한다거나 A[1..4] 중 최솟값, 최댓값을 빠르게 구하는 등 다양한 용도로 사용할 수 있다.

구간 트리는 이진 트리 형태로 구성되고, 각 트리의 노드가 일차원 배열의 특정 구간을 대표하게 된다. 배열 a[10]이 있다면 아래 그림과 같이 구간 트리를 구성할 수 있다.

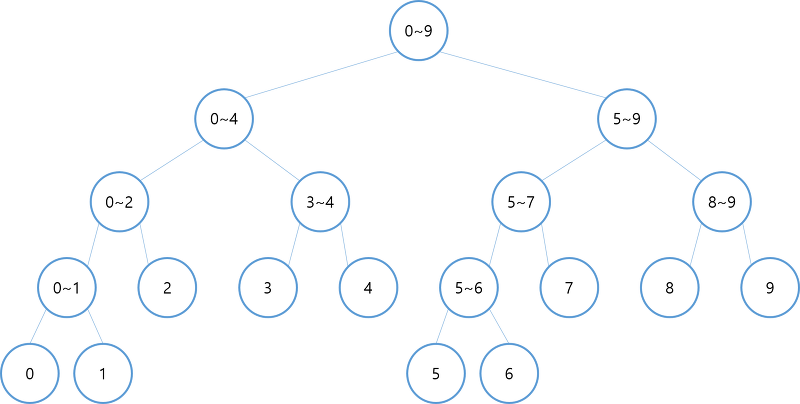
segment-tree

이와 같은 구간 트리는 배열 A에 대하여, 다음과 같은 작업을 반복적으로 수행할 때, 효율적으로 사용할 수 있는 자료구조가 된다.

특정 구간 A[l..r]의 합(또는 최댓값, 최솟값 등)을 구하는 작업
A[k]번째 수를 변경하는 작업

구간 합 트리는 아래와 같이 구현할 수 있다. 구간 최대, 최소 트리도 원리는 같기 때문에 구현하기 어렵지 않다.

struct SegmentTree {
  vector<int> tree;

  SegmentTree(vector<int>& arr) {
    //assert(!arr.empty());
    tree.assign(arr.size() * 4, 0);
    build(arr, 1, 0, arr.size() - 1);
  }

  void build(vector<int>& arr, int id, int l, int r) {
    if (l == r) {
      tree[id] = arr[l];
      return;
    }
    int m = (l + r) / 2;
    build(arr, id*2, l, m);
    build(arr, id*2+1, m+1, r);
    tree[id] = tree[id*2] + tree[id*2+1];
  }

  void update(int pos, int diff, int id, int l, int r) {
    if (pos < l || pos > r) return;
    if (l == r) {
      tree[id] += diff;
      return;
    }
    int m = (l + r) / 2;
    update(pos, diff, id*2, l, m);
    update(pos, diff, id*2+1, m+1, r);
    tree[id] = tree[id*2] + tree[id*2+1];
  }

  int query(int ql, int qr, int id, int l, int r) {
    if (ql > r || qr < l) return 0;
    if (ql <= l && r <= qr) return tree[id];
    int m = (l + r) / 2;
    return query(ql, qr, id*2, l, m)
         + query(ql, qr, id*2+1, m+1, r);
  }
};

Lazy Propagation

기본적인 구간 트리의 구현에서는 특정 구간의 값을 일정하게 변경할 때 트리의 루트부터 말단 노드까지 타고 내려가 해당하는 말단 노드들의 값을 모두 변경하는 방식을 사용한다. 예를 들어 [l..r] 구간의 값들에 3씩 더하려면 위에서 구현한 코드로는 update(l, 3), update(l+1, 3), …, update(r-1, 3), update(r, 3)을 해주어야 한다. 구현을 조금 다르게 해서 한 번의 호출로 [l..r] 구간을 모두 업데이트하게 만들어 조금 빠르게 만들 수도 있겠지만 결국 트리의 말단 노드까지 모두 내려가야 하므로 이러한 연산의 시간복잡도는 \(O(nlog_2n)\)이 된다. 이와 같은 방식이 이해하기 쉽지만, 너무 느리다는 단점이 있다.

구간 트리의 각 노드는 특정 구간의 값들을 대표한다. 어떤 구간의 값들을 갱신하려고 할 때, 일단 해당 구간을 대표하는 노드의 값만 갱신하고, 이 노드의 자식 노드들은 나중에 갱신이 꼭 필요할 때 해주면 이 작업을 보다 빠르게 수행할 수 있다. 아래 코드와 같이 각 노드에 대해 갱신에 필요한 정보를 저장하는 정보를 저장해두면 이와 같은 작업을 비교적 간결하게 구현하게 있다.

struct SegmentTreeLazyPropagation {
  vector<int> tree, lazy;

  SegmentTreeLazyPropagation(const vector<int>& arr) {
    //assert(!arr.empty());
    tree.assign(arr.size() * 4, 0);
    lazy.assign(arr.size() * 4, 0);
    build(arr, 1, 0, arr.size() - 1);
  }

  void build(const vector<int>& arr, int id, int l, int r) {
    if (l == r) {
      tree[id] = arr[l];
      return;
    }
    int m = (l + r) / 2;
    build(arr, id*2, l, m);
    build(arr, id*2+1, m+1, r);
    tree[id] = tree[id*2] + tree[id*2+1];
  }

  void propagate(int id, int l, int r) {
    if (lazy[id] != 0) {
      tree[id] += (r - l + 1) * lazy[id];
      if (l != r) {
        lazy[id*2] += lazy[id];
        lazy[id*2+1] += lazy[id];
      }
      lazy[id] = 0;
    }
  }

  void update_range(int ul, int ur, int diff, int id, int l, int r) {
    propagate(id, l, r); 
    if (ul > r || ur < l) return;
    if (ul <= l && r <= ur) {
      tree[id] += (r - l + 1) * diff;
      if (l != r) {
        lazy[id*2] += diff;
        lazy[id*2+1] += diff;
      }
      return;
    }
    int m = (l + r) / 2;
    update_range(ul, ur, diff, id*2, l, m);
    update_range(ul, ur, diff, id*2+1, m+1, r);
    tree[id] = tree[id*2] + tree[id*2+1];
  }

  int query(int ql, int qr, int id, int l, int r) {
    propagate(id, l, r);
    if (ql > r || qr < l) return 0;
    if (ql <= l && r <= qr) return tree[id];
    int m = (l + r) / 2;
    return query(ql, qr, id*2, l, m)
         + query(ql, qr, id*2+1, m+1, r);
  }
};

연습 문제

RSQ

BOJ 4297 Ultra-Quick Sort (문제 보기)

역전의 수(Inversion)의 수를 세는 문제로 0번 원소부터 N-1번 원소까지 각 원소를 구간 트리에 1로 업데이트 해주는데, 이 때 i 번 원소는 [ 0 ~ i-1 ] 번 원소들 중 자신보다 큰 원소의 수를 구간 합 트리를 이용하여 셀 수 있다.

BOJ 13334 철로 (문제 보기)

모든 철로의 시작과 끝 x 좌표들을 압축한 배열 X와 이에 대응하는 구간 합 트리를 만들고, 각 철로의 끝 지점에서 철로의 시작 지점에 해당하는 X 배열 위치에 1로 업데이트 해주고, (끝 지점 - L, 끝 지점)에 해당하는 구간에 쿼리를 날려 이 구간에 포함되는 철로의 수를 세면 된다.

BOJ 3653 영화 수집(문제 보기)

m+n개 원소의 구간 합을 저장하는 구간 합 트리를 만든다. 그리고 [m ~ m+n-1] 번 원소의 값을 1 (존재함을 의미)로 만들어 준다. 그리고 어떤 DVD x 를 뺄 때, 이 x 의 구간 트리 상의 위치를 R 이라고 하면 R의 값을 0으로 업데이트 해주고 구간 (0, R-1) 의 합을 쿼리를 통해 x의 위에 있는 DVD의 총 수를 구할 수 있다.

BOJ 1280 나무 심기 (문제 보기)

구간 합 트리를 두 개 사용하면 된다. 하나는 단순히 해당 좌표에 나무가 몇 개 있는지를 저장하는 구간 트리 cTree, 다른 하나는 x = 0 에서부터 해당 위치까지 거리, 즉 x = 1 에는 1, x = 3 에는 3, x = X[i] 에는 X[i]를 저장하는 구간 트리 sTree. 그러면 나무를 X[i] 에 심는데 필요한 비용(현재 심어져있는 모든 나무 까지 거리의 합)은 lcnt \(\times X[i]\) - lsum 과 rsum - rcnt \(\times X[i]\) 을 합해서 얻을 수 있다. 여기서 lcnt, rcnt, lsum, rsum이 의미하는 바는 다음과 같다.

lcnt: cTree 에 구간 [0 , X[i] - 1] 쿼리 결과, 즉 왼쪽에 심어져 있는 나무의 개수
rcnt: cTree 에 구간 [X[i]+1, MAX_X] 쿼리 결과, 즉 오른쪽에 심어져 있는 나무의 개수
lsum: sTree 에 구간 [0, X[i] - 1] 쿼리 결과, 즉 x = 0부터 왼쪽에 심어져 있는 나무들까지의 거리 총합
rsum: sTree 에 구간 [X[i]+1, MAX_X] 쿼리 결과, 즉 x = 0 부터 왼쪽에 심어져 있는 나무들까지의 거리 총합

BOJ 1655 가운데를 말해요 (문제 보기)

특정 원소가 있으면 1로, 없으면 0으로 배열에 대응하는 구간 합 트리를 이용하면 k 번째 원소를 찾을 수 있다.

int kth(int k, int id, int l, int r) {
  if (l == r) return l;
  int m = (l + r) / 2;
  if (tree[id*2] >= k)
    return kth(k, id*2, l, m);
  else
    return kth(k-tree[id*2], id*2+1, m+1, r);
}

RMQ

BOJ 1753 최단경로 (문제 보기)

간단하게 다익스트라로 풀 수 있는 문제인데, 다익스트라를 구간 트리로 구현할 수 있다. 우선순위큐에서 최단거리로 갈 수 있는 정점을 꺼내는 작업을 구간 최소 트리로 구현할 수 있다. 이미 최단 거리를 구한 정점은 트리에 INF로 업데이트해주면 된다.

BOJ 5480 전함 (문제 보기)

모든 전함의 시작, 끝 x 좌표와 수직으로 발사하는 레이저의 x 좌표로 구성된 X 배열과 이에 대응하는 구간 최소 트리 xTree 를 만들고, 마찬가지로 모든 전함의 y 좌표와 수평으로 발사하는 레이저의 y 좌표로 구성된 Y 배열과 이에 대응하는 구간 최소 트리 yTree 를 만든다.

그리고 각 수직, 수평 레이저의 배열 X, Y 위치에 레이저 번호 (빨리 발사되는 레이저일 수록 작은 번호)로 값을 갱신해준다. 이 때, 같은 위치에서 같은 방향으로 발사하는 레이저는 먼저 발사된 레이저의 값으로 해주어야 한다. 그런 다음에는 각 전함의 시작 x 좌표, 끝 x 좌표로 구간 트리 xTree 에 쿼리를 날리고, 마찬가지로 시작 y 좌표, 끝 y 좌표로 구간 트리 yTree 에 쿼리를 날리면 자신을 파괴하는 레이저를 찾아 낼 수 있다.

BOJ 3745 오름세 (문제 보기)

lis 를 찾는 문제이다. 0 번 원소부터 N-1 번 원소까지 순회하면서 자신을 끝으로 하여 만들 수 있는 최대 lis 의 길이를 구간 트리에 업데이트 해준다. 이 때 i 번 원소는 [0 ~ i-1 ] 번 원소들 중 자신보다 작은 원소를 끝으로 하는 최대 최대 lis 의 길이를 구간 최대 트리로 찾을 수 있다.

BOJ 1365 꼬인 전깃줄 (문제 보기)

전깃줄을 꼬이지 않게 줄들을 선택해 나가기 위해서는 좌측 1번부터 이에 대응하는 우측 전봇대를 항상 오름차순으로 선택해 나가면 된다. 즉 lis 를 구하는 문제와 같아진다. 위의 오름세 문제와 같은 방식으로 풀면 된다.

BOJ 9345 디지털 비디오 디스크(DVDs) (문제 보기)

L번 선반부터 R번 선반까지 L번 DVD부터 R번 DVD까지 모두 있는지는 구간 (L, R) 의 최솟값이 L이고, 구간 (L, R) 의 최댓값이 R 인지를 확인하면 알 수 있다.

Lazy propagation

BOJ 2934 LRH 식물 (문제 보기)

먼저 가능한 모든 x 좌표로 구간 합 트리를 만든다. 매일 매일 나무를 심는 작업은 [L+1, R-1] 구간의 값을 모두 1로 만들면 되고, 꽃이 몇 개 피는지는 L 과 R 의 쿼리를 날려 얻을 수 있다. 꽃이 핀 부분은 다시 0으로 업데이트 해주면 된다. 구간 값 갱신을 \(O(log_2N)\)에 수행하는 Lazy propagation 구간 합 트리 구현이 필요한 문제이다. 또는 펜윅 트리를 사용하면 보다 쉽게 구현이 가능하다.

BOJ 1395 스위치 (문제 보기)

BOJ 12844 XOR (문제 보기)

BOJ 7626 직사각형 (문제 보기)

참고 자료

프로그래밍 대회에서 배우는 알고리즘 문제해결전략, 구종만
Competive Programming 3, Steven Halim
https://www.acmicpc.net/blog/view/9
https://www.acmicpc.net/blog/view/26

No Silver Bullet