No Silver Bullet

평방 분할 기법(Square Root Decomposition)

sqrt root decomposition

Square Root Decomposition

우리 말로는 평방 분할이라고 불리는 이 기법은 특정 구간에 대한 질의(query)에 빠르게 답하기 위한 기법(일종의 자료구조라고 볼 수도 있다)이다. 먼저, 아래와 같은 문제에 대해 고민해보자.

원소의 개수가 \(n\)개인 배열 a[]가 있다. 이 배열에 대해서 \(q\)개의 질의(query)가 하나씩 들어오는데 질문의 내용은 다음 2가지 중 하나이다.

  1. 특정 구간 \([l, r]\)의 합을 구하라.
  2. 특정 위치 \(idx\)의 값을 \(val\)로 변경하라.

위와 같은 문제는 단순하게 반복문을 이용하여 \(l\)부터 \(r\)까지 순회하면서 값을 더해나가면 구할 수 있다(시간복잡도: \(O(q \times n)\)). 그런데 \(q\)개의 질의에 대한 답을 하다 보면, 이미 예전에 계산해두었던 어떤 구간의 합을 또다시 계산하는 상황이 나오기 마련이다. 평방 분할 기법은 이러한 중복 계산을 최소화하기 위해 고안되었다.

평방 분할 기법의 핵심 아이디어는 아래와 같이 크기 \(n\)의 배열을 크기 \(\sqrt n\)의 여러 블록으로 나누어 각 블록에 해당하는 구간 합을 미리 계산해두고, 구간 \([l, r]\)의 합을 계산할 때 \(l\)과 \(r\)사이에 완전히 포함되어 있는 블록들에 해당하는 구간은 미리 계산해두었던 구간 합을 바로 사용하여 불필요한 중복 계산을 없애는 것이다.


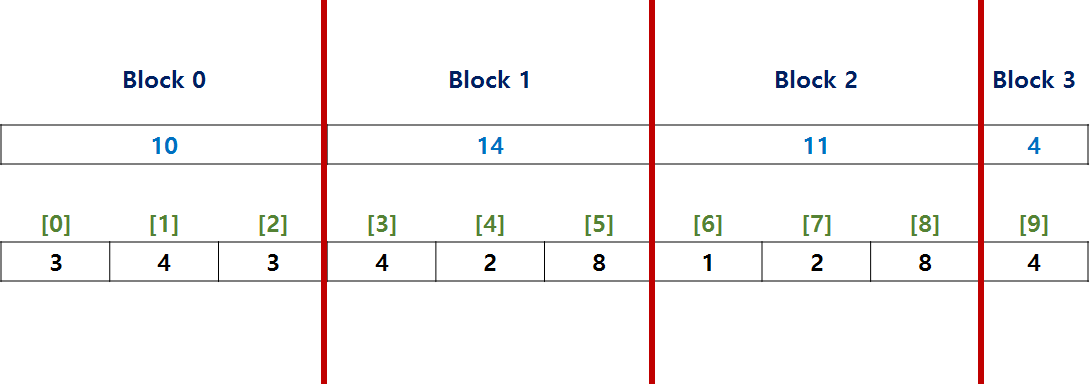
square_root_docomposition


시간복잡도는 계산해보면 구간 합을 구하는 질의에 대해서 구간에 완전히 포함되는 블록에 해당하는 구간 합을 구하는데 \(O(\sqrt n)\)이 소요되고, 포함되지 않는 구간을 직접 순회하면서 계산하는데 \(O(2 \times \sqrt n)\)의 시간이 소요된다. 그리고 특정 위치 값을 갱신하는 작업의 경우 간단하게 배열 값과 해당하는 블록 값만 갱신해주면 되므로 상수 시간에 수행 가능하다. 따라서 총 \(q\)개의 질의에 대한 전체 시간복잡도는 \(O(q \times \sqrt n)\)이 된다.

int arr[MAX_N];
int block[MAX_SQRTN];
int blksz;

void preprocess(int input[], int n) {
  int blk_idx = -1;
  blksz = (int)sqrt(n);
  for (int i = 0; i < n; i++) {
    arr[i] = input[i];
    if (i % blksz == 0) blksz++;
    block[blk_idx] += arr[i];
  }
}
int query(int l, int r) {
  int sum = 0;
  int lb = l / blksz, rb = r / blksz;
  if (lb == rb) {
    for (int i = l; i <= r; i++) {
      sum += arr[i];
    }
  } else {
    for (int i = l; (i / blksz) == lb; i++) {
      sum += arr[i];
    }
    for (int i = lb + 1; i < rb; i++) {
      sum += block[i];
    }
    for (int i = r; (i / blksz) == rb; i--) {
      sum += arr[i];
    }
  }
  return sum;
}
void update(int idx, int val) {
  int block_number = idx / blksz;
  block[block_number] += val - arr[idx];
  arr[idx] = val;
}

연습 문제

CF 785E Anton and Permutation

참고 자료

  • http://www.geeksforgeeks.org/sqrt-square-root-decomposition-technique-set-1-introduction/

Related Posts